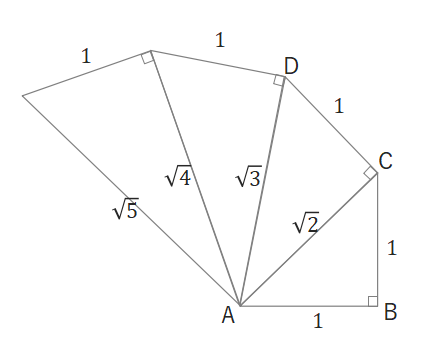
今回の記事では三平方の定理を利用して、平方根の長さを作図する方法を解説しています。
\(\sqrt{3}\)、\(\sqrt{5}\)、\(\sqrt{6}\)、\(\sqrt{7}\)の求め方を知りたい人は参考にしてください。
平方根の長さの作図1 正方形を利用して√3を作図しよう
1辺の長さが1の正方形を利用して\(\sqrt{3}\)を作図します。

BDに対角線をひくと、\(BD=\sqrt{2}\)になります。
対角線の長さがすぐに思いつかなくても、△ABDはAB=AD=1、∠B=90\(°\)の直角三角形であることからもBDの長さが求められます。

BCの延長上にBD=BC’となる点C’をとります。(BDの長さをコンパスではかって印をつけてください。)このとき\(BC’=\sqrt{2}\)となります。

さらに\(C’\)から垂線をひき、\(BC’D’=90^\circ\)、\(C’D’=1\)となるような点\(D’\)をとります。

BとD’を結ぶと∠C’=90\(°\)の直角三角形BC’D’ができます。
三平方の定理より\(BC’^2+C’D’^2=BD’^2\)となるので、\(BD’^2={(\sqrt{2})^2+1^2}=3\)、\(BD’=\sqrt{3}\)となります。

これで\(\sqrt{3}\)の作図ができました。
平方根の長さの作図2 √5、√6、√7を作図してみよう
\(\sqrt{3}\)の作図で三平方の定理を利用しましたが、同様に三平方の定理を利用すれば、\(\sqrt{5}\)、\(\sqrt{6}\)、\(\sqrt{7}\)…の長さも作図で求められます。
直角三角形の斜辺を利用すれば√5、√6、√7が作図できる!
直角三角形の斜辺を\(x\)とおくと三平方の定理より、
斜辺が\(x\)、その他の辺が\(1\)、\(\sqrt{2}\)のときは
\(x^2=1^2+(\sqrt{2})^2=3\)より、\(x=\sqrt{3}\)
斜辺が\(x\)、その他の辺が\(1\)、\(\sqrt{3}\)のときは
\(x^2=1^2+(\sqrt{3})^2=4\)より、\(x=\sqrt{4}=2\)
斜辺が\(x\)、その他の辺が\(1\)、\(2(=\sqrt{4})\)のときは
\(x^2=1^2+2^2=5\)より、\(x=\sqrt{5}\)
斜辺が\(x\)、その他の辺が\(1\)、\(\sqrt{5}\)のときは
\(x^2=1^2+(\sqrt{5})^2=6\)より、\(x=\sqrt{6}\)・・・
というように、斜辺でない辺の一方を1に固定してもう一方の辺の√の中の数を1増やすごとに、斜辺の長さも√の中の数が1ずつ増えていきます。これを利用します。
正方形を利用して√5、√6、√7を作図する
上の\(\sqrt{3}\)の作図問題に続けて、\(\sqrt{3}\)の作図と同じように\(2(=\sqrt{4})\)も作図します。
BD’=BC”となるような点C”をBCの延長上にとります。さらに\(C’’\)から垂線をひき、\(BC’’D’’=90^\circ\)、\(C’’D’’=1\)となるような点\(D’’\)をとります。これで\(BD’’=2\)となります。
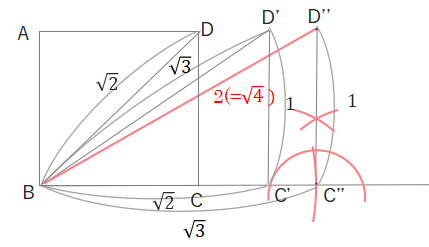
これをくり返していけば、\(\sqrt{5}\)、\(\sqrt{6}\)、\(\sqrt{7}\)も作図できます。(くわしい手順は省きます。)
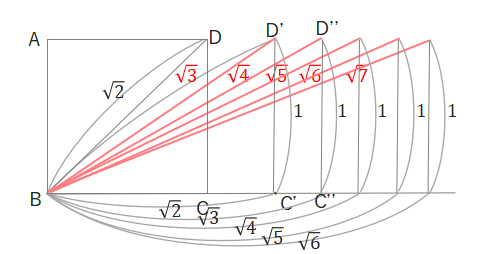
直角三角形の斜辺をつなげて√3、√5、√6・・・を作図する
直角三角形の斜辺を1辺にした直角三角形をつなげていき、平方根の長さを作図することもできます。(こちらも細かな作図の手順は省略、考え方のみ解説します。)
AB=AC=1、∠B =90\(°\)の直角三角形を利用して、\(\sqrt{3}\)を作図で求めます。

Cを通りACに垂直で長さが1となる線分CDをひき、∠ACD=90\(°\)となる直角三角形ACDを作ります。三平方の定理より\(AD=\sqrt{3}\)となります。
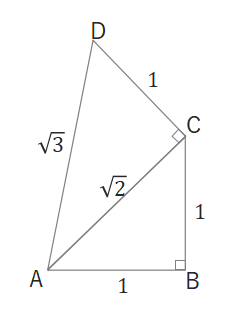
これをくり返せば\(\sqrt{4}\)、\(\sqrt{5}\)・・・と作ることができます。